
Neural Digits (Python)
A simple neural network that allows users to train, test, and perform digit recognition on the MNIST dataset with over 99% accuracy with sufficient training. Users can train from scratch, use a saved model, and use their own images for digit prediction.
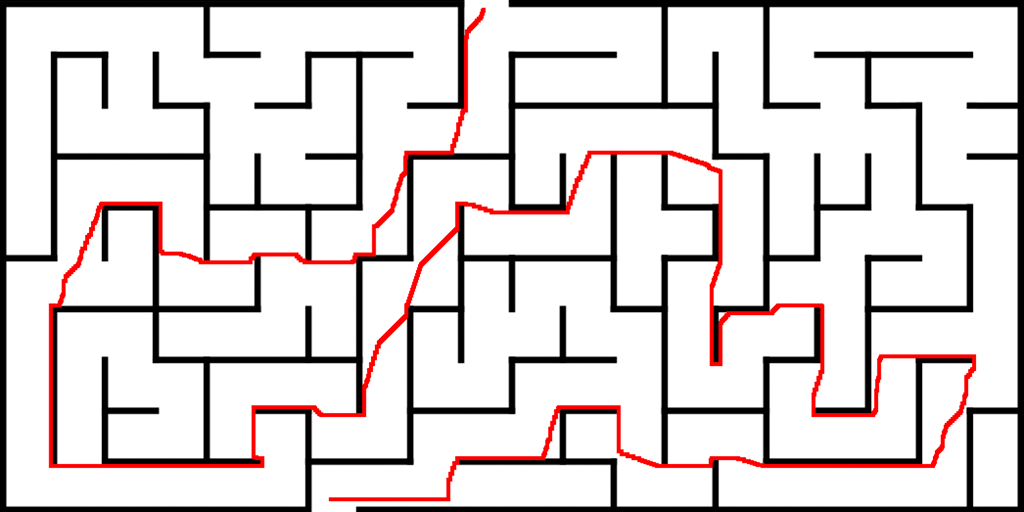
Custom Maze Solver (JavaScript)
Allows the user to upload an image of a maze (or choose a premade one), then finds a shortest (Manhattan) pixel path between two chosen points by using Dijkstra’s algorithm.

Markov Chain Text Generator (JavaScript)
Lets the user enter a sample text, then generates text that is similar to it by using a first-order Markov chain.

3D Wireframe Engine (Java)
A simple 3D engine that uses the drawLine() method from the Java Graphics library and Euler angles to render an interactive wireframe environment from scratch. Use the arrow keys and QWEASD to navigate.

Wolfram Spiral Automaton (JavaScript)
A cellular automaton inspired by Stephen Wolfram’s elementary cellular automaton rules. Here, the the cell wanders outward in a counterclockwise spiral in an infinite square grid. For each step, its color (among three possibilities, by default) is determined by the colors of its eight adjacent cells. The rule (which is displayed by setting verbose=true in the URL) for how coloring is performed is randomized by default, but can be specified in the URL via the parameter rule (i.e. append &rule=3c… to the URL). Here is a gallery of some generated images.

Julia Set Randomizer (PHP)
Generates random Julia set PNG images using the PHP GD Graphics Library. Adjust the image size with the width and height parameters, and experience unique fractal patterns with each refresh. Explore the source code or generate multiple Julia sets simultaneously.
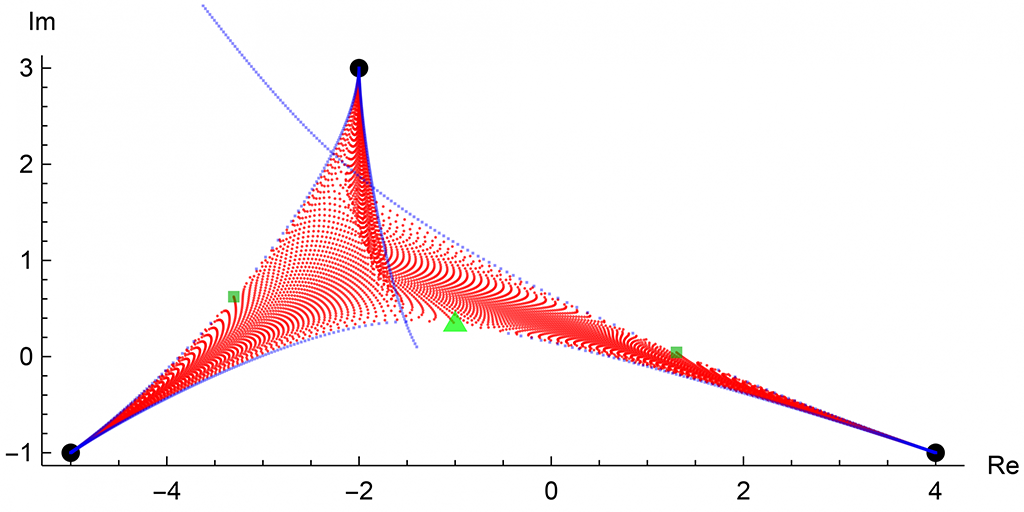
Polynomial Shadow (Mathematica)
Takes a univariate polynomial P and plots shadow(P,n), i.e. the union of all zeros of all orders of the derivative of Pⁿ, where n is a fixed natural number. In the plot, the large dots and squares are the zeros and critical points of P, respectively, the triangle is the center of mass of the zeros of P, and the small squares are the branch points of equations (1.3) and (1.4) in the z-plane in my paper that the program is based on. Here is the code in text format, and here is a gallery of some shadows.